Cylinder:

The simple solids considered in Engineering Mechanics may be, cone, cylinder, sphere, hemisphere etc. The surface areas plus the volumes of some of these solids are computed below.

Cylinder

(i) Consider a be the radius of a cylinder and H be its height. Suppose the axis of cylinder to be along z axis as illustrated in Figure.

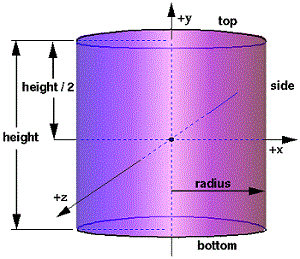
Figure

In this case, we may consider the generator as straight line AB of length H, which while rotates around z-axis forms a cylinder as illustrated in the above figure.

In this particular case, the centroid G of length AB is at mid-point of AB.

                        x¯  (at G) = a

Through the First Theorem of Pappus & Guldinus,

Surface of cylinder        ∴ = L × ( x¯ θ)

                                               S = L × a θ

For full revolution θ = 2 π

Surface        S = 2 π a L

 (ii)       To find out the volume of cylinder consider the plane area OBAC illustrated shaded, where O and C are the centres of circles traced by points B and A, respectively. The volume of cylinder is produced when this area rotates around z-axis (that means OC).

Now,    Area OBAC = A = H × a

The centroid of this area is equal to GA, where x co-ordinates is (a/2).

 Using Theorem II

Volume of Cylinder =  A × ( x¯ θ)

= H × a × 2 π ×  (a /2)

V = π a ²  H