Cone:

 (i) A cone is produced when an inclined length AB = L revolves around z-axis which is taken along with OA, the axis of the cone.

The centroid GL of length L is at the mid height where, x¯_L = a/2 as observed in Figure.

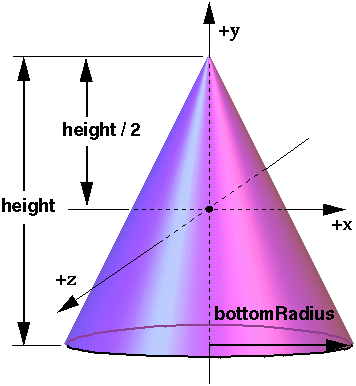
{Cone surface generated  by the length AB about the axis OA }= L × ( x¯ _L  θ)

            where,     θ = 2 π

                          x _L   =  a/ 2

∴ Cone surface = L × (a/2) × 2 π

                                  ∴ = π a L

(ii) Solid volume of cone is obtained when plane area AOB is revolved about axis OA. The centroid G_A of the plane area ABO is at

Volume of cone = Area ( AOB) × x¯_A  θ

=  (Ha/2) ×  (a /3)× 2 π = π a² H/3