Find the support reactions:

Find the support reactions and draw the BM and SF diagrams of the continuous beam shown in Figure EI = constant.

Solution

The positive bending moment diagram (due to external loads) for the two spans, the area of the M/EI   diagrams and CG distances are shown in Figure 19(b). In the case of support moment diagrams shown in Figure 19(c), M_A = 0 and M_C = 0, only M_B is unknown and is assumed to be M. The support M/EI   diagram is shown at Figure 19(c). As there are no support movements, all the Δ's are zero. Hence, the equation of three moments Eq. (2.25(b)) is reduced to:

0x 6/EI +2M(6/EI+12/EI)+0x12/EI+6x(90x3/EIx6)+6x(360x6/EIx12)=0

giving M = - 37.5 kNm.

To find reaction R_A, take moments of forces left of B. This gives: BM at B = R_A. 6 - 20 × 3 = - 37.5 giving R_A = 3.75 kN.

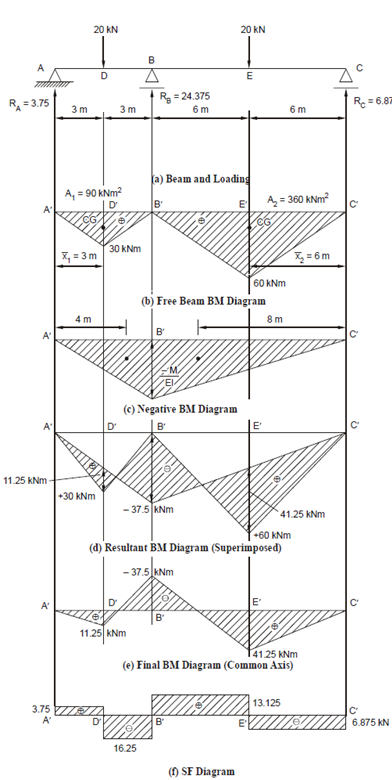
Similarly, taking moment of forces right of support B :

BM at B = R_C. 12 - 20 × 6 = - 37.5 giving R_C = 6.875 kN.

Also, ? ∑V ≡ 0, R_A  + R_B  + R_C  = 20 + 20

∴ R_B = 40 - 3.75 - 6.875 = 29.375 kN

The BM diagrams are shown in Figures (d) and (e) and the SF diagrams in Figure (f).