White Test:

We  now consider the White's test of heteroscedasticity proposed by  Hal White (1980). From the OLS estimates we can find out the residuals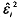.  Suppose we use the regression residuals  to run  the following regression:  

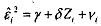
from which we cdculate  the measure  of goodness  of  fit, R2.  The White's test  is  based on the fact that when there is homoscedasticity,

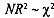
with 1 degree of freedom. More generally, when  there arep  independent Z variables, the distribution will havep degree of freedom. Note that White's test is  very general. To carry  it out we need not make any specific assumptions about the nature of heteroscedasticity. Obviously it gives us some advgintage -  we can test  for every form of heteroscedasticity through thik  test.

However. we are exposed  to  the psk that the power of  the White's test is often bad so that the null hypothesis gets too often  rejected. The White's test is also sensitive to specification bias, that is, if any relevant variable  is omitted from the model. In addition, the White's  test is non-constructive  in the sense that when we reject the null hypothesis  this test does not offer any suggestion regarding future course of action.