Goldfeld-Quandt Test:

The Goldfeld-Qwdt  test is  qpplicable  if heteroscedasticity is related to only one of the explanatory vdableo. Suppose in our regression model the error variance' increases Hiith the regressor x₁.  In  order to carry out the Goldfeld-Quandt test we proced as follows:

• arrange the observations  in increasing order of x,
• omit some observations  (say, r out of n  observations) in the middle of  the data series
• run a  regression on  the first n₁  =  (n-r)/2  observations, obtaining  the error sum of squares, ESS,
• run a regression on the last n₂  =  (n-r)/2  observations, obtaining the error sum of squares, ESS,  
• test  the null hypothesis 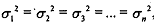by using the F-test for the test statistic 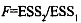for degrees  of  freedom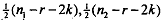

The omission  of  r observatioris  from  the data set  is  required.for  the G-Q  test. There is no hard and fast rple for the exact value-of  r and the choice  is  quite aubitrary. In practice, about one fourth observations, are omitted.