Durbin-Watson Test:

A popular test for detecting autocorrelation is  the Durbin and Watson test statistic defined as  

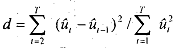
which is simply the ratio of the sum of squared differences in successive residuals to the overall error sum of squares (ESS).

If this was based on the true u,  and T waq very largc  then dcan  be shown  to  tend in the limit as T  gets large  to 2(1-p).  This means that if ρ->0,  then d->2;  if ρ->1 then d->0 and if ρ->1  then d-> 4. Therefore a  test for II₀, : ρ =  0,  can be based on whether d  is close to 2  or not. Unfortunately, the critical values of d  depend upon the X, and these vary  fiom one data  set to another. To get around  this, Durbin and Watson established upper (d₀) and lower (d_L) bounds for this critical value. It is obvious that if the observed d is less than the lower bound d_L or larger I  than (4  -  d_L),  then we can safely reject H_o.

On the other hand if the observed d  is between d_i,  and (4 -  d₀) then we do no1 reject the hypothesis. If d lies in any of the two indeterminate areas, then one should compute the critical values depending on X.  Most econometric software packages report the Durbin-Watson statistic automatically along with the p-value, that is the level of  significance of this statistic (in general for  the 5%  level of testing if  the p-value  is less than  0.05 then you can  reject the null  hypothesis  of no autocorrelation).

If we are interested in a one-tailed test, say  H_o : p =  0 versus H₁  :  p > 0, that is positive autocorrelation only, then we would reject H_o  if d <  d_L,  and not reject H_o, if d_L <  d_U.  If on  the other hand d_L< d< d_L then  the test is  inconclusive. Note that with a one tailed test only one side of the earlier test is operational. The conditions are still  the same;  the only  difference is we  ignore one set of conditions. With a two-tailed test we reject Ho  based on both where d  lies and where (4-4 lies. Here we are interested only in the value of d since we are testing only for positive autocorrelation versus the null of no autocarrelation. Earlier the alternate hypothesis was any type of autocorrelation. Similarly, for testing H_o : p  =  0 versus H,  :  p <  0, we compute (44  and follow the same steps as before while testing for negative autocorrelation. Here our alterna~e  hypothesis  in only negative autocorrelation,  versus the null of no autocorrelation.