Breusch-Godfrey Test:
A more powerful test that is also commonly used in empirical applications is the Breusch-Godfrey (BG) tyst, also known as the LM test. Using our earlier example of a single variable with intercept model the test proceeds in the following way. Note in this context that there can be many more variables as regressors, one variable case is taken for simplicity only. Similarly, lagged values of the dependent variable etc. can also be there as a regressor. Assume that the error term follows the p-th order autoregressive, AR(p) scheme (extension of the earlier AR(1) scheme), as follows
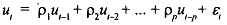
where E, is a stochastic error as before. The null hypothesis to be tested is:
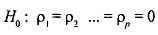
In it is hypothesized that there is no autocorrelation of any order. The BG test involves the following steps:
1) Estimate by OLS and obtain the residuals ti,
2) Regress ui, on the original x, (as well as any other variables used as regressors ealier) and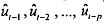 
where the latter are lagged values of the estimated residuals in step 1. Thus if p=4, we will introduce four lagged values of the residuals as additional regressors in the model. In short, run the following regression:
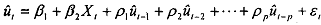
and obtain from this the auxiliary egression.
3) If the sample size is large then Breusch and Godfrey have shown that
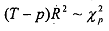
where T is the total.number of observations. That is the BG test statistic is asymptotically (as the sample size increases to infinity) distributed as a chi- squared distribution withp degrees of freedom. Therefore, once the test statistic has been calculated this way it can be compared to a standard chi-squared distribution to accept or reject the null hypothesis of no autocorrelation of any order.
Note that unlike the Durbin-Waton test the BG test can test for both higher order schemes of the error process AR(p) not just AR(1). It also is applicable when alternate time series for the error term is specified such as ,a Moving Average scheme. MA(p), is defined as follows
