Isoparametric Curves on Bezier Surface:

In the parenthesis, the expression involves basis functions B_n,j (u) and control points p_i,j. Note down that the basic functions do not depend on i; but the control points do. Thus, we may define a new function q_i (v) to reflect this fact :

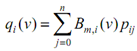
Clearly, each q_i (v) is a Bézier curve described by control points p_i0, p_i1, . . . , p_in (that means the i-th row of control points). As a consequence, we have m + 1 new points q₀(v), q₁ (v),. . . , q_m (v). As v is fixed and may be considered as a constant, points q₀ (v), q₁ (v), . . . , q_m(v) will not alter positions as u changes. As a result, the surface equation becomes

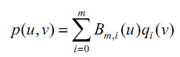
As v is fixed, p(u, v) is in fact a single variable parametric equation in u and therefore represents a curve on the surface. It is a Bézier curve in u described by m + 1 control points q₀ (v), q₁ (v), . . . , q_m(v).

Thus, we conclude that any isoparametric curve along with v fixed is a Bézier curve described by a set of control points that may be computed from the equation of the surface. Interchanging the role of u and v, we shall have the similar conclusion for isoparametric curves in the v direction. Figure illustrated isoparametric curves on a Bézier surface in both of the directions.

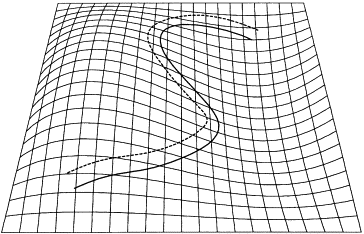
                     Figure: Isoparametric Curves on Bezier Surface