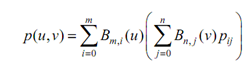Important Properties:
Many important properties of Bézier surfaces are listed here. These properties may be proved easily by applying the similar techniques utilized for Bézier curves. Please compare these significant properties with those of Bézier curves. Remember the equation of a Bézier surface :
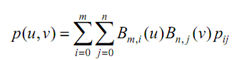
Here the two one-dimensional basis functions are described as follows :
B m,i(u) = (m!/ i!(m - i)! ) ui (1 - u)m-i
B n, j (v) = (n! / j !(n - j)! ) vi (1 - v)n-i
- p (u, v) passes from the control points at the four corners of the control net : p0,0, pm,0, pm,n and p0,n.
- In fact, we have p (0, 0) = p0,0, p (1, 0) = pm,0, p (0, 1) = p0,n and p (1, 1) = pm,n .
- Non-negativity : B m,i (u) Bn,j (v) is nonnegative for all m, n, i, j and u and v in the range of 0 and 1.
This is obvious.
- Partition of Unity : The addition of all Bm,i (u) Bn,j (v) is 1 for all u and v in the range of 0 and 1.
More precisely, it means for pair of u and v in the range of 0 and 1, the following holds:
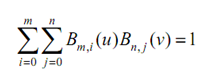
• Convex Hull Property : A Bézier surface p(u, v) lies in the convex hull described by its control net.
As p(u, v) is the linear combination of all of its control points along with positive coefficients which sum is 1 (partition of unity), the surface lies in the convex hull of its control points.
• Affine Invariance : it means that to apply an affine transformation to a Bézier surface one may apply the transformation to all of control points and the surface described by the transformed control points is identical to the one attained by applying the similar transformation to the surface's equation.
• Variation Diminishing Property : No such thing presents for surfaces. Isoparametric curves on a Bézier surface, actually on any tensor product surface, contain a extremely easy structure. In the equation of a Bézier surface, basis function B m,i (u) only based on the index i and may be taken out of the summation in j. Therefore, the equation has the following form :