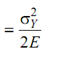Toughness

When the load acts upon the specimen, certain work is done. This work it stored in the specimen as its strain energy. If load P acts upon the specimen and causes certain displacement, dL the work completed,

U = ∫ P dL                                            

If either side of above equation is divided by volume

 U/ A₀ L₀ = ∫ (P / A₀) (dL / L₀) = ∫ σ d ε  

The integral ∫ σ d ε is nothing but the area under stress-strain curve. It means that the work done upon the specimen per unit volume during stretching, which is stored in the specimen as strain energy, can be measured by area under the curve. The maximum elastic energy per unit volume that material can absorb without attaining plastic state is known as "modulus of resilience", whereas the energy stored in the specimen at any stress in elastic limit might be referred to as resilience.

The toughness of a material is understood to be its ability to absorb energy during entire elastic & plastic deformation. The "modulus of toughness" is measured as area under entire stress-strain curve and is the energy absorbed by material of the specimen per unit volume up to fracture.

From Figure it can be seen that modulus of toughness will depend upon both the ultimate tensile strength and strain at fracture and material which is very ductile will exhibit a higher modulus of toughness as is the case with mild steel. On the other hand, modulus of resilience depends upon yield strength (or proportional limit or elastic limit) and hence a material with higher yield strength will have higher modulus or resilience. Higher toughness is a desirable property in materials used for gears, chains, hooks, freight car coupling etc. Higher resilience is desirable in springs.

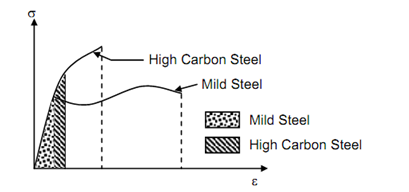
                   Figure: σ - ε Curves for High Toughness (Mild Steel) and Low Toughness (High Carbon Steel) Materials

For ductile materials like mild steel the modulus of toughness may be calculated by approximate formula:

Modulus of toughness = σ_u ε_f =   (σ_Y + σ_u)/2 ε_f             

Where σ_Y & σ_u are respectively yield and final tensile strengths, and ε_f is the strain as fracture. Modulus of reliance is the area of triangle whose height is σ_Y and base is the strain corresponding to σ_Y, i.e. ε_Y. Hence modulus of resilience is ½ σ _Y ε_Y.

Since  ε_Y   =    σ_Y/E

Modulus of resilience