Bezier Curve:

Bezier curves are utilized in CAD and are named after a mathematician functioning in the automotive industry. Bezier curves are depending on approximation method that produces curves that do not pass through all the specified data points except the first and the final control point. A Bezier curve does not needs first-order derivative; the shape of the curve is controlled through control points.

Since in the previous section, we let one segment of the curve. For n + 1 control points, the Bezier curve is represent by a polynomial of degree n as:

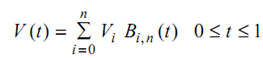         -------(1)

here V (t) is the position vector of a point on curve segment & B_i, n are the Bernstein polynomials, that serve as the blending or fundamental function for the Bezier curve.

The Bernstein polynomial is represents as

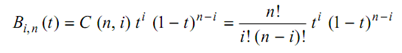---------(2)

Here C (n, i) is the binomial coefficient provide by

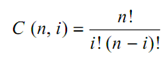---------- (3)

Putting Eq. (2) in Eq. (1)

Where V₀, V₁, . . . , V_n are the position vectors of n + 1 points that make the so-called characteristic polygon of the curve segment.

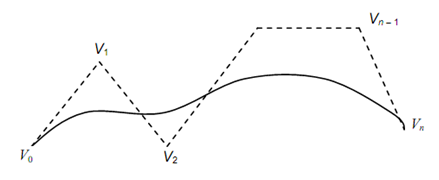
            Figure: Bezier Curve and its Characteristic Polygon