Parabolically Blended Surface of Revolution:

Let the parabolically blended curve described by the points P₁ [0 1 0], P₂ [2 3 0], P₃ [4 1 0], P₄ [5 2 0]. Rotate this curve around the x-axis through 360^o to attain a surface of revolution. Determine the surface point at u = 0.5 and φ = 60^o = π/3.

By using Eqs.( 13) and (14), the parametric equation of the surface of revolution is

                   Q (u, φ) = [T] [A] [G] [S]

 putting the value of [S], [T], [A] and [G]

For t = 0.5 & φ = π/3 (60^o)

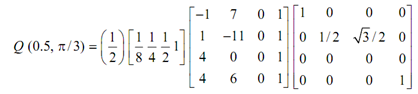
=     [ 49/16  33/32  33√3/32 ]    = [3.0625   1.03125   1.786181   1]

The resulting surface can be the design of a even or bowl a wind tunnel or rocket nozzle.