Bezier Surface:

A tensor product Bezier surface is refers to an extension of the Bezier curve in two parametric directions u and v.

A Bézier surface is described by a two-dimensional set of control points p_i,j, where i is in the range of 0 and m, and j is in the range of 0 and n. Therefore, in this case, we have m + 1 rows and n + 1 columns of control points and the control point on the i- th row and j-th column is denoted by p_i,j. Note down that we have (m + 1) (n + 1) control points in total.

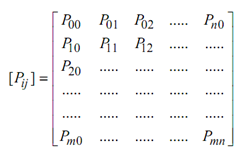
An orderly set of data or control points [P_ij] is utilized to build-up a topologically rectangular surface as illustrated in Figure.

The surface equation of a Bézier surface indicated by m + 1 rows & n + 1 columns of control points :

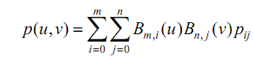
0 < u  < 1, 0 < v < 1

where B_mi (u) and B_n,j (v) are the i-th & j-th Bézier basis functions in the u- & v- directions, respectively. Recall from Bézier curves, these basis functions are described as follows :

B_{m ,i} (u) =  (m! / ( i!(m - i)! ))    uⁱ (1 - u)^m-i

B_{n ,j} (u) =  (n! / ( j!(n - j)! ))    vⁱ (1 - v)^n-i

P (u, 0) is any point on the surface and P_ij are control points. These points make the vertices of control or characteristic polyhedron as illustrated by dotted lines in Figure . Since B_m,i (u) and B_n,j (v) are degree m and degree n functions, we will say this is a Bézier surface of degree (m, n). The set of control points is generally referred to as the Bézier net or control net. Note  down that parameters u and v are in the range of 0 and 1 and therefore a Bézier surface maps the unit square to a rectangular surface patch.