Synthetic curve:

Any synthetic curve such like cubic, parabolically blended, spline, Bezier and B-spline curves may also be rotated to produce surface of revolution. Figure illustrated a surface of revolution built up by using a relatively simple parabolically blended curve. A parametric space curve in the matrix form is following:

                                                    P(u) = [T] [N] [G]

Here [T], [N] and [G] are respectively parameter, blending function and geometry matrices,. The general form of the matrix equation for a surface of revolution is following

               Q(u, φ) = [T] [N] [G] [S]

here [S] represents the contribution because of rotation around an axis by the angle π. For a particular case of rotation around the x-axis,

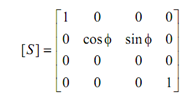
Rotate around the y-axis by + 90° to form the a-axis coincident with the x-axis.

The above three steps are required only to find out the inverse transformations needed to place the surface of revolution correctly in three space. Having produced the surface of revolution by rotation around the x-axis, the following three steps right place it in three space :

•  Translate in x to place the centre of the surface of revolution at the correct position on the a-axis.
•  By apply the inverse of the combined rotation transformations to the surface of revolution.
•  Perform the inverse of translation of the point a₀ to the surface of revolution.

 A point on the surface of revolution is then specified by

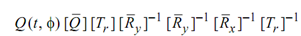
where   R_x = Rotation matrix about x-axis,

            R_y = Rotation matrix about y-axis, and

           T_r = Transformation.