Surface Energy:

If we wish to increase the area of the liquid surface, we will have to do work (apply force) to stretch it and this work will have to be done against the surface tension. To find an expression for the work to be done, consider a rectangular wire frame MNPO (Figure) in which the wire OP is movable. Now Let l is the

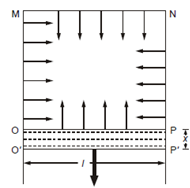
Figure: Soap Film on a Rectangular Frame

length of the wire OP. If we dip this frame in soap solution, a soap film is formed. Because of surface tension, a soap film pulls a wire OP inward. From Eq. (1.1), this force can be written as:

 Force = σ × 2 l

where σ denotes the surface tension of the film. Note that we have multiplied the length of the wire by a factor of 2 because the soap film touches the wire OP above as well as below. Suppose that a force is applied on the wire OP such that, the film stretches from position OP to O' P' by a small distance x. Thus, the work done on the wire OP can be written as:

Work Done = Force × Displacement

= σ× 2 l × x

= σ × Δ s

where Δ s (= 2 l × x) is the total increase in the surface area of the soap film. This work is stored as the surface energy in the soap film. Further, Eq. (1.3) can be written as :

Surface Tension (σ) = Work Done/Area

= Surface Energy/Area

Therefore, we can also define surface tension as surface energy per unit area of the surface.

You must have noticed that, in discussing surface tension, we used the concepts of mechanics such as force, work and energy. Similarly, other static and dynamic properties of liquids can be explained using the concepts of mechanics such as force, pressure, density and velocity. In the next section, you will study one of the most important properties namely hydrostatic pressure. You will also learn the Pascal's law and Archimedes principle which govern the behaviour of fluids at rest.