Sweep Surfaces:

 A three-dimensional surface is also attained by traversing an entity, for example a line, polygon or curve, along with a path in space. The resulting surfaces are called as sweep surfaces. Sweep surface generation is often utilized in geometric modelling. The simplest sweep entity is a point. The result of sweeping any point along with a path is, of course, not a surface but a space curve. Though, it serves to illustrate the fundamental technique.

Let the position vector P [x  y  z  1] swept along with the path represented by the sweep transformation [T_s]. The position vector Q (s) representing the resulting curve is

                            Q (s) = P [T_s]          s₁ ≤s < s₂            -------- (16)

The transformation [T_s] find out the shape of the curve. For instance, if the path is a straight line of length n parallel to the z-axis, then

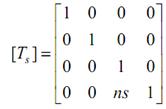
                                                                                         0 ≤ s ≤ 1

 If the path is an origin-centered circle in a z = constant plane, then (see in below Eq.)

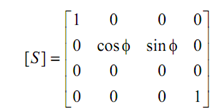
According to this

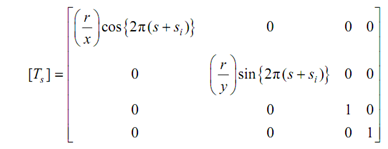
                                                                                                                    0 ≤ s ≤ 1

whereas s_i = (1/2π) tan_-1 (y_i/x_i) and for P [x  y  z  1], r = 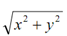. Here, the subscript i is utilized to mention the initial or begining point.