Ruled Surfaces:

Ruled surfaces, also called as "lofted surfaces", are both simple and fundamental to surface design. They are of considerable significance in their own right, in specific for the design of "functional" surfaces in mechanical engineering. Ruled surfaces solve out the following problem: given two space curves c₁ and c₂, both described over the same parameter interval u ∈ [0, 1], determine a surface x that contains both curves as "opposite" boundary curves. More precisely: search x such that

p(u, 0) = c₁ (u),  x(u, 1) = c₂ (u)

 Obviously, the stated problem has infinitely several solutions, so we pick the "simplest" one :

p(u, v) = (1 - v) c₁ (u) + v c₂ (u),

or, with Eq.:       

p(u, v) = (1 - v) x (u, 0) + v x (u, 1)

Ruled surfaces contain the familiar flavor of linear interpolation: every isoparametric line u = const is a straight line segment, as shown in Figure.

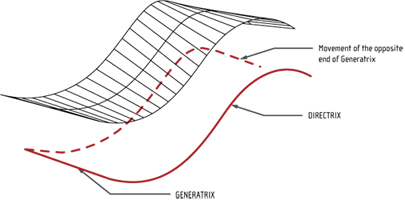
The difference through earlier occurrences of linear interpolation is that we interpolate now to whole curves, not just discrete points - therefore this process is frequently referred to as transfinite interpolation. It is yet quite manageable, though: note down how the linear terms in v are kept separate from the data terms in u.

An significant aspect of ruled surfaces of the form of Eq. is the generality that is permitted for the input curves p(u, 0) and p(u, 1) : there is virtually no limitation on them other than with to be defined over the same parameter interval. For example, one of the input curves may be a cubic polynomial curve, the other a spline curve or even a polygon.