Non-parametric curves:

In the second case, while there is no pre-existing object to model, the user creates the object in the modelling procedure; therefore, the object matches its representation exactly, because its just embodiment is the representation. To build the object, the user can sculpt the object interactively, explain it mathematically, or give an approximate shape.

Surface may be defined mathematically in 3-D space by non-parametric and parametric equations.

∴ The equation of surface is p (x, y, z)

                 p (x, y, z) = [x, y, z] ---------------(1)

                  where   z = g (x, y).

The natural form of z is a polynomial passing through all of the points, that is

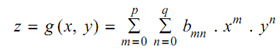                    -------------- (2)

whereas the surface is explained by an xy grid of size (p + 1) × (q + 1) points. There are two popular methods of fitting non-parametric surfaces. One is by fitting a surface passing through all the data points, the other one is to make a series of surface patches taking some set of data points into consideration and afterwards all such surface patches are associated with C₀ and C₁ continuity. Eqs. (1) and (2) hold good for surface patches as well.

Non-parametric surfaces suffer from all of the disadvantages compared to parametric surface same to non-parametric curves.

A general 3-D surface may be modelled by dividing it into an assembly of topological patches. A patch is a basic mathematical element to model a composite surface. A surface may be composed by a single patch or assembly of many patches.