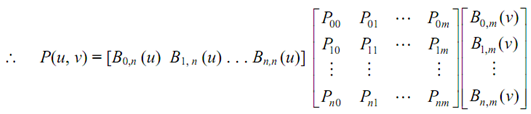Example: A 3 × 3 Bezier Surface Computation:

 A cubic Bezier surface may be attained by substituting n = 3 and m = 3 in

Eqs. 19-26

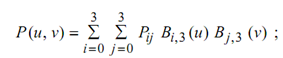
                                                                                                0 ≤ u ≤ 1, 0 ≤ v ≤ 1

This equation may be expanded to give

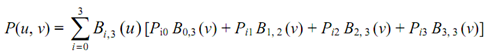
= B_0,3 (u) [P₀₀ B_{0, 3} (v) + P₀₁ B_{1, 3}(v) + P₀₂ B_{2, 3} (v) + P₀₃ B_{3, 3} (v)]

+ B_{1, 3} (u) [P₁₀ B_{0, 3} (v) + P₁₁ B_{1, 3} (v) + P₁₂ B_{2, 3} (v) + P₁₃ B_{3, 3} (v)]

+ B_{2, 3} (u) [P₂₀ B_{0, 3} (v) + P₂₁ B_{1, 3} (v) + P₂₂ B_{2, 3} (v) + P₂₃ B_{3, 3} (v)]

+ B_{3, 3} (u) [P₃₀ B_{0, 3} (v) + P₃₁ B_{1, 3} (v) + P₃₂ B_{2, 3} (v) + P₃₃ B_{3, 3} (v)]

 This equation may be written in a matrix form as

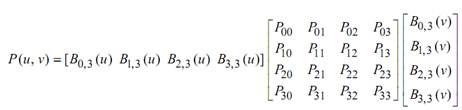
or        

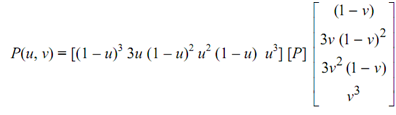
P(u, v) = U^T  [M_B] [P] [M_B]^TV

where the subscript B indicate Bezier and

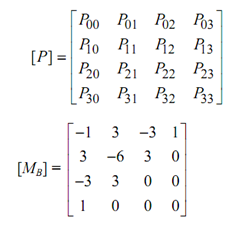
and the U and V vectors are [u³   u²   u 1]^T respectively. Note that [M_B] is the same matrix for the cubic Bezier curve.

U^T [M_H] [B] [M_H]^TV = U^T [M_B] [P] [M_B]TV

 [M_H] [B] [M_H] = [M_B] [P] [M_B]^T

or Solving out  for [B] gives [MH^{]- 1}. This equation may be reduced to give

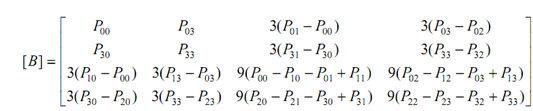
Comparing this equation along with Equation for the bicubic patch reveals that the tangent and twist vectors of the Bezier surface are expressed in terms of the vertices of its characteristic polyhedron.