B-Splines Surface:

A tensor product method for B-spline surface is same to Bezier surface. This is an extension of B-spline curve in two parameter definition in u and v.

A B-spline surface may be constructed from the following information:

1. a set of m + 1 rows and n + 1 control points p_i,j, where 0 ≤ i ≤ m and 0 ≤ j ≤ n;

2. a knot vector of h + 1 knots in the u-direction, U = {u₀, u₁, . . . , u_h};

3. a knot vector of k + 1 knots in the v-direction, V = { v₀, v₁, . . . , v_k };

4. the degree p in the u-direction; and

5. the degree q in the v-direction;

The B-spline surface described by the above information is the following :

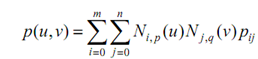
Here N_i,p (u) and N_j,q (v) are B-spline basis functions of degree p and q, respectively. Note down that the fundamental identities, one for each direction, should hold: h = m + p + 1 and k = n + q + 1. Thus, a B-spline surface is another instance of tensor product surfaces. Since in Bézier surfaces, the set of control points is generally referred to as the control net and the range of u and v is 0 and 1. Therefore, a B-spline surface maps the unit square to a rectangular surface patch.