Supply Curve of Industry:

The industry supply can be obtained by summation of the supply of all the  firms. Therefore, the industry supply would be,

     S = Σ q_i (p) over all N firms, where i = 1,2,...N

If the firms are all identical then qi(p) is the same for all. Assuming q_i = q, total industry supply would be S = N.q   

The industry supply curve S implies the summation of all the individual supply curves of the existing firms in the market.

A Numerical Example

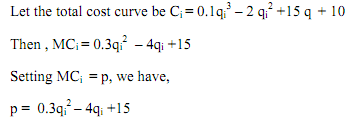
This is a quadratic equation in qi, therefore,

q_i = [4+ (10+1.2p)]/0.6  [4- (10+1.2p )]/0.6

The individual firm's supply function is relevant for all p≥ minimum AVC.  

The AVC function is AVC_i  = 0.1qi² - 2q_i +15  
The minimum point on the AVC is located by taking derivative with respect to qi and setting the derivative equal to zero, as shown below.

d (AVC_i)/dq_i = 0.2q_i - 2 = 0  

Therefore,

 q_i = 10.

Substituting q_i = 10 in the AVC function we get,

minimum AVC = 5.

Therefore, the firm supply function is  

S_i =  [4 ±  (1.2p - 2)]/0.6 ]                               for p ≥ 5

    = 0                                                               for p < 5

If the industry consists of 100 identical firms, the aggregate supply function is

S = 100× [4 ±  (1.2p - 2)]/0.6                         for p ≥ 5
    = 0                                                               for p < 5

At a price of 22.5, the aggregate supply would be 1500 units.