Limitations of superposition Theorem
• Superposition theorem does not work for power computation. Since power computations include the product of current or voltage, the square of current or the square of voltage, they are not linear operations. This statement can be described with an easy illustration as given below.
Example: Consider the circuit diagram as shown in figure below.
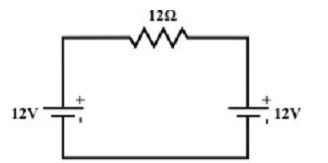
By using superposition theorem one can find the resulting current flowing via 12Ω resistor is zero and thus power consumed by the resistor is also zero. The power consumed in an any resistive element of a network cannot be calculated by using the superposition theorem. Note that the power consumed by each separate source is given by,
PW1(due to 12 V source(left)) 12 Watts; PW2 (due to 12 V source(right) 12 Watts
The total power consumed by 12 Ω = 24watts (by applying superposition theorem). This outcome is wrong theoretically. However, we might use the superposition theorem to find a current in any branch or a voltage across any branch, from which power is, then, can be computed.
• Superposition theorem cannot be exerted for non linear circuit (i.e., Transistors or Diodes).
• This technique has weaknesses: - In order to compute load current IL or the load voltage VL for numerous choices of load resistance RL of the resistive network, one requires resolving for every source voltage and current, possibly numerous times. With the simple circuit, this is pretty simple though in a large circuit this technique becomes a sore experience.