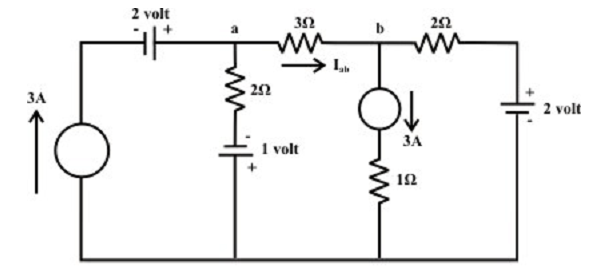
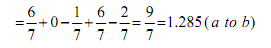Compute the current Iab flowing via the resistor 3 Ω as shown in figure below by using the superposition theorem.

Solution: 

Suppose that the current source 3A (from left to the 1 volt source) is acting all alone in the circuit and the internal resistances substitute the other sources. The current flowing via the 3Ω resistor can be acquired from the figure shown below.    

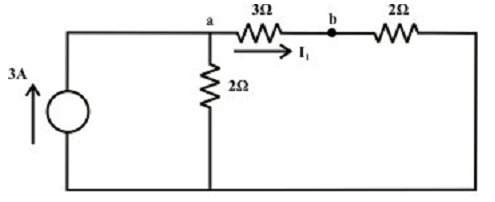
and it is acquired by,
I₁ (due to 3 A current source) = 3 x 2/7 = 6/7 A (a to b)

The current flowing via 3 Ω resistor due to 2V source can be acquired from the figure shown below. 

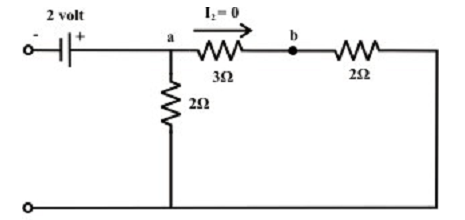
and it is observed from no current is flowing. 
I₂ (due to 2 v voltage source) = 0 A (a to b)

The current via 3Ω resistor due to 1V voltage source only (as shown in figure below) is acquired by

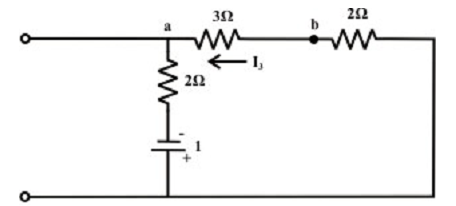
I₃ (due to 1 v voltage source) = 1/7 A (b to a)

The current via 3Ω resistor due to 3 A current source only (as shown in figure below) is acquired by,

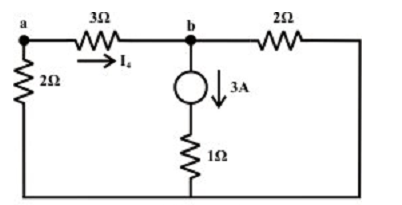
I₄ (due to 3 A current source) = 3 x 2/7 = 6/7 A (a to b)

The current via 3Ω resistor due to 2V voltage source (as shown in figure below) is acquired by,

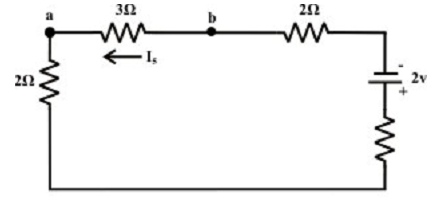
I₅ (due to 2 V voltage source) = 2/7 A (b to a)

The resulting current Iab flowing via 3Ω resistor due to the grouping of all sources is acquired by the expression below (the algebraic sum of all currents acquired in the above equations with correct direction of currents)

I_ab = I₁(due to 3 A current source) + I₂(due to 2 v voltage source) + I₃(due to 1 v voltage source) + I₄ (due to 3 A current source) + I₅ (due to 2 V voltage source)