Q: Determine the value of V₀ in given circuit.

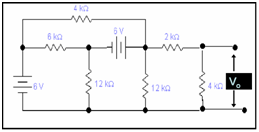
Answer:       The circuit can be redrawn like

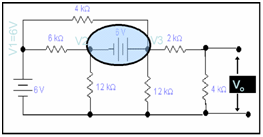
Node 2 & 3 constitute a super node, with constraint equation

                                                   V₃ - V₂ = 6V

                        By applying KCL equation at super node

                         ((V₂ - 6)/6k) + (V₂/12k)+ ((V₃-6)/4k)+ (V₃/12k) + (V₃/6k) = 0

                        (V₂/6k) + (V₂/12k) + (V₃/6k) + (V₃/12k) + (V₃/4k) - (6/4k) - (6/6k) =0

                                                       (V₃/2k) - (30/12k) + (V₂/4k) =0

                                                               3V₂ +6V₃ - 30 =0

                                                                        V₂ + 2V₃ =10 ..........(1)

                        Now, from the constraint equation of super node

                                                                        V₂ =V₃ -6

                        KCL equation (1) of super node become

                                                                        3V₃ - 6 =10

                                                                           V₃ = 16/3 volts

                                                                                 V₂ = (16/3) - 6 = - 2/3 volts      

                        By applying voltage division rule

                                                             V₀ = (4k x V₃)/(2k + 4k)

                                                                       = 64/18 = 3.55 V   Ans.