Sum-of-Product (SOP) Equation:
SOP equation is a function of Boolean variables, which define the fundamental product terms or minterms, which shall give a high output for the given inputs. For example, the output Y is a function of three Boolean variables A, B and C whose minterms are listed which shall give a high outputs.
Y = F (A, B, C) = ∑ m (1, 2, 3, 4) = A¯ B¯ C + A¯ B C¯ + A¯ B C + A B¯ C¯
Let us attempt to determine the truth table from the given SOP equation. Tabulate all the possible values of A, B and C in the order of enhancing minterm index i. In the truth table, place 1s whose minterms are tabulated in the SOP equation and at the other places draw 0s as in Table
Table: Truth Table for SOP Equation
|
A
|
B
|
C
|
Minterms
|
Y
|
|
0
|
0
|
0
|
m0
|
0
|
|
0
|
0
|
1
|
m1
|
1 ( A¯ B¯ C)
|
|
0
|
1
|
0
|
m2
|
1 ( A¯ B C¯ )
|
|
0
|
1
|
1
|
m3
|
1 ( A¯ B C)
|
|
1
|
0
|
0
|
m4
|
1 (A B¯ C¯ )
|
|
1
|
0
|
1
|
m5
|
0
|
|
1
|
1
|
0
|
m6
|
0
|
|
1
|
1
|
1
|
m7
|
0
|
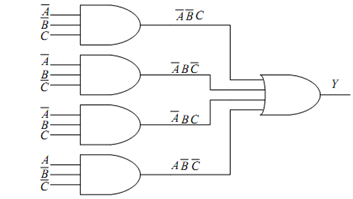
Figure: Logic Circuit for SOP Equation