Expressions for the bursting and resisting forces:

We may write the expressions for the bursting & resisting forces as below.

The pressure working on the inner curved surface of the shell acts normal to the surface and therefore, it shall be acting in all of directions. The vertical components of the bursting force is attained by letting a small ring ABCD subtending an angle dθ at the centre as illustrated in Figure .

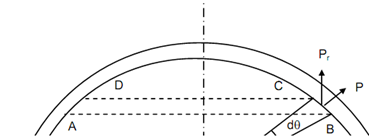
Figure

Resolving the normal force because of the internal pressure working on this elemental ring vertically, we have

dP = p × ((d/2) × d θ) (π × 2 × (d/2) cos θ )× sin θ

Therefore, the total vertical component of the bursting force in the hemispherical shell shall be

= (π/4 ) pd ²

The vertical resisting force because of the hoop stresses acting on the reaction shall be

R =π dt σ_h

As the equilibrium is maintained by the activity of the two forces, they should be equal and opposite. Therefore, we get

    R = P_v

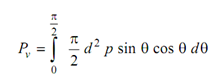
 Therefore, we get (π/4) dt σ_h  = π pd ²

σ_h  = pd/ 4t

Likewise, considering any other diametrical plane section cutting the shell, the hoop stresses in the shell shall be found to be the similar both in nature and magnitude because of the symmetry of the shell. Therefore, it may be understood that the hoop stress in any direction in thin spherical shell is given by the following expression :

σ_h  = pd/ 4t      (tensile)