General State of Stress in Two Dimensions:

Since a general state of stress in two dimensions is defined by the stress components σ_x, σ_y and τ_xy, as shown in Figure, general expressions for normal and shear stress components may be obtained by algebraic sum of the respective components from Eqs. (22) to (29), as given below:

σ_n = σ_x cos² θ + σ_y sin² θ +2 τ_xy cos θ sin θ

τ_nt = - σ_x cos θ sin θ + σ_y cos θ sin θ + τ_xy (cos² θ - sin² θ)

On further simplification, we obtain

σ_n = ((σ_x + σ_y)/2) + ((σ_x - σ_y)/2) cos 2θ + τ_xy sin 2θ                                             . . . (30)

τ_nt = ((σ_y - σ_x)/2) sin 2θ + τ_xy cos 2θ                                                                       . . . (31)

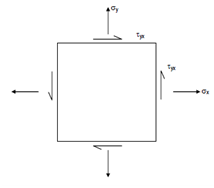
Figure: General State of Stress in Two Dimensions

Application of Eqs.(30) and (31) will be elaborately dealt along here. Therefore, the significance of the equations should be stressed at this stage. While we are carrying out stress analysis on solids, we might be evaluating stress elements on a set of mutually perpendicular planes, such as σ_x, σ_y and τ_xy. The magnitudes of these components might not always be enough to decide whether the solid is safe or not, and we need evaluation of stress elements on other specific planes, or determination of planes on that the stress elements have extreme value. Such an analysis could be simply carried out with the help of Eqs. (30) and (31).