Bending Stress Distribution:

Bending Stress

The bending moment at a section tends to bend or deflect the beam. The internal stresses resist the bending. The resistance offered by the way of internal stresses to the bending is called bending stress. The theory, relating bending along bending moments and bending stresses, is said the theory of bending. Now, in this section, you will also see the pattern of bending stress distribution across the cross section of the beam.

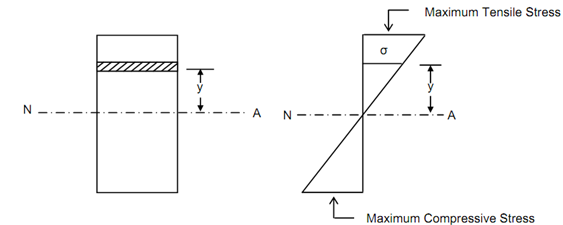
Let us assume an elemental area da at a distance y from the neutral axis as shown in Figure .

 The stress on the elemental area, σ = (E/ R) × y

Force on the elemental area    = σ da

= ( E / R) × y da

Moment of resistance offered by the elemental area = Force × Distance

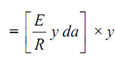
         Cross-section of Beam            Stress Distribution Diagram

Figure

Total moment of resistance, M, offered by the beam = ∑ (E/ R )× y² da

=  (E/ R)  Σ y² da

But Σ y² da is the moment of inertia I of the beam section around the neutral axis.

∴          M =  (E/R) I

               M/ I = E/ R                         ---------(1)

Earlier, we have seen that, σ = (E/ R)  × y,

or         σ / y = E/ R                             ------------- (2)

From Eqs. (1) and (2), we obtain

M / I = σ / y = E/ R

Let us consider the equation M/ I = σ/ y ,

where,

M = bending moment at a section,

I = moment of inertia of the beam section,

σ = stress on any layer of beam, and

y = distance of the layer from neutral axis.

M and I are constants for a particular beam section. Hence, it may be concluded that the stress σ varies proportion to the distance y. It is a linear variation. Thus maximum stress occurs at extreme fibres. The stress distribution diagram shall be a triangle as illustrated in Figure. For the cantilever subjected to a clockwise moment M, maximum tensile stress will occur at the topmost fibre and maximum compressive stress shall occur at the bottom-most fibre.