Stress-Strain Relationship of Solid

In order to know the stress-strain relationship of the solid more apparently, further tests are carried out by unloading, loading and reloading of the solid at many stages and results of such an investigation are illustrated in given Figure.

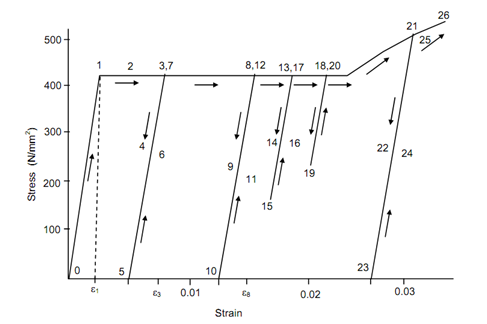
From the results of such a study the following observations may be made.

1. When the loading is completed in the proportional limit of the solid, the strain (deformation) caused is completely recovered while the stress is removed. (If the load is partially eliminated, a proportional amount of strain gets relieved.)
2. While the solid is loaded beyond yield limit & then unloaded; just a part of the strain is relieved and a considerable part of strain still persist therefore effecting permanent changes in the geometry of the solid. The strain remaining unrelieved is called as permanent set.
3. While we reload a solid that is already subjected to permanent set, the stress-strain curve for reloading is linear up to the maximum stage to which it was subjected to earlier.

From these observations, what does a designer learn? If a structure or any element is loaded beyond proportional limit, the geometry gets permanently modified and if repeatedly loaded beyond proportional limit, it shall go totally out of shape after a few repetitions. Conversely, you might load it within their proportional limit any number of times and the original geometry recover on the elimination of the load. Therefore, in any design, one ought to be careful to ignore loading the component beyond the proportional limit. In this limit the solid is said to be elastic. The property called as elasticity consists of two aspects, in general complete elimination of strains on unloading and linearity of stress-strain relationship. Therefore, the part of stress-strain curve up to yield point is also called elastic limit. To ensure that the solid is always in this elastic limit, designers permit stresses in solid much lower than the elastic limit. The ratio of the maximum stress a material might withstand to the maximum stress that a designer select to allow is called the factor of safety. In short,

Factor of Safety = Maximum stress the material can withstand/ Maximum stress permissible

If the numerator is yield point stress, a factor of security is 2 generally permitted and if it is final stress, factor of safety might be 3 or more.

All of materials don't act as mild steel. The stress-strain curves of a little material are illustrated in given Figure. Irrespective of the variety of shapes seen in these curves, one might recognize in each of them a segment where the curve might be considered linear. This restriction is taken as the elastic limit for the material.

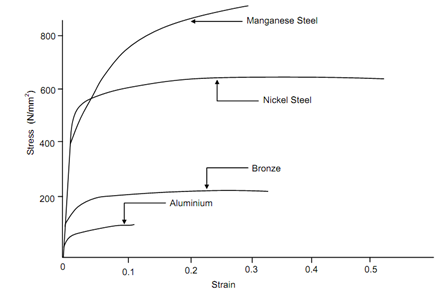
                                                            Figure: Stress-Strain Relationship for a Few Materials

The whole behaviour of the material and its whole stress-strain relationship is discussed here only in order to caution the designer to keep the stress level well in the elastic limit. Therefore, for practical purposes the stress-strain relationship is taken as linear & during the rest of this course you shall not be dealing with nonlinearity of material behaviour. Therefore, for a designer, stress is always proportional to the strain & the proportionality constant is described as Elastic Modulus.

Therefore, Stress, σ = Elastic Modulus (E) × Strain (ε)

Equation 1   σ = E . ε         

From Eq. (1), we obtain

Equation 2  E = σ/ ε                                     

Eq. (2) mentions that the Elastic Modulus of a material might be calculated by measuring the slope of the stress-strain curve (in the elastic limit). The fact that Eq. (1) holds good in elastic limit that has already been taught to you as Hooke's Law, which we might restate as follows: In elastic limit the strain generated in a solid is always proportional to the stress applied.