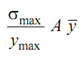Analysis of Partial Beam Section:

Until now, we have seen forces & moments acting over the whole cross-section of the beam. Now, let us assume a part of the beam section and attempt to establish a relation for the normal force working on the partial beam section & the moment of the normal force regarding the neutral axis.

Normal Force

Consider a beam section as illustrated in Figure.

Consider σ_max be maximum bending stress at the topmost layer and y_max be the distance of the top most layer from the neutral axis.

Let us discover the normal force on a partial area A, illustrated shaded in Figure. In that shaded area, consider da be an elemental area & y be its distance from the neutral axis.

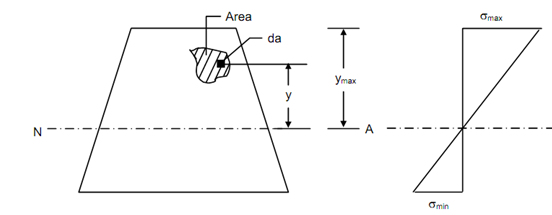
                                        Beam Section                           Bending Stress Distribution

 Figure

The stress, σ on elemental area is proportional to the distance y.

σ = σ_max  ×(y/ y_max)

Normal force on the elemental area = σ × da

= σ_max (y/ y_max)

Total normal force on the shaded area = ∑ σ_max (y/ y_max)

                                                             = (y /y_max) ∑ y da

Let be the distance of the centroid of the shaded area from the neutral axis.

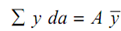
∴ Normal force on a partial beam section =