Deflection of Beams:

Deflection is explained as the vertical displacement of a point on a loaded beam.

Slope is explained as the angle among the deflected central line and original central line of the beam.

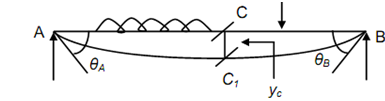
Illustration

From Figure,

y_c = Deflection at point c.

The beam is replaced by central line of neutral plane. The bent form of this central line is known as elastic curve of beam. The expression for elastic curve is in the form of y = f (x) where y is the deflection at x.

θ_A = Slope at A,

θ_B = Slope at B,

ACB = Original beam, and

AC′B = Deflected beam.

Figure

The deflections of beams are extremely significant in the design of structures. The excessive deflection cause cracks in ceilings, cracks in walls, make a feeling of lack of security and affect shape, geometry and appearance. In machine parts, such as shafts might result in undesirable interference among mating parts such like gears. Therefore, the maximum deflection is minimized in the design.

Objectives

After leaning this unit, you must be able to

• conceptualise the deflections,
• determine the deflection & slope of simply supported beams,
• determine the deflection & slope of cantilevers, and
• determine the deflection and slope of other determinate beams.