Change in Volume of Cylinder:

To discover the volumetric change (ratio of change in volume to be original volume) the expression for the volume of the cylinder shall be considered.

Volume is given by,

V = (π d ²/4) × l

On differentiating, we obtain change in volume,

δV  =    (π d ² / 4 )δl  + (π /4)× l × 2d × δd

Therefore,  Ratio change in volume/ Original volume

= δV/  V

 (We do not to describe this ratio as volumetric strain, as the volume of the material that makes cylinder is not the internal volume of the cylinder. This volume is the volume of any particular substance enclosed in space of the cylinder, and δV/ V   with mean the volumetric strain of that substance. This strain then shall be associated to pressure and bulk modulus of the substance.)

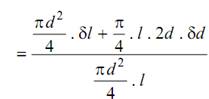
=   ((π d ²/4) . δl  + (π /4). l . 2d . δd ) / ((π d ² /4). L)

=          δl/ l + 2 (δd / d) = ε_l  + 2εh

Therefore,

 ε_v  = ε_l  + 2ε_h

=   (pd /4tE ) (1 - 2v) + 2 ( pd /4tE  ) (2 - v)

=   (pd /4tE) (1 - 2v + 4 - 2v)

=   (pd /4tE)  (5 - 4v)

Therefore, the volumetric strain is attained as the sum of longitudinal strain & twice the hoop strains.

In terms of the pressure, diameter and thickness volumetric strain may be expressed as,

ε_v = (pd /4tE)  (5 - 4v)

Now we will see some examples for finding out the strains and deformations in thin cylindrical shells.