Concept of Strain Energy:

From some previous units, we know that while a deformable body is subjected to external forces the body internally produce stresses & strains. For instance, if we apply a compressive force on a spring, the spring deforms producing internally shear stresses and shear strains. At the similar time we observe that the point of application of the compressive force moves by a distance of the spring deflection (amount of contraction). We also know that this compressed spring contain a facility to do work while released. It means that a certain amount of energy is stored in the spring in its strained state. Previous we noted down that work was done on the spring by the compressive force. Now, while we link the above two statements we realise that the work completed on the spring is transformed into energy stored in it by virtue of the strain in the spring. This form of energy emanating out of the internal strain in the body is known as strain energy. Therefore, strain energy is a specific form of potential energy which is stored up within materials which have been subjected to strain as a result of work done on the material.

Also, we have seen that strain energy,

U = external work done.

Therefore, for a slowly applied load the work done in straining the body is specified by the shaded area under the load-extension graph of Figure 1.

U = (½) P Δ

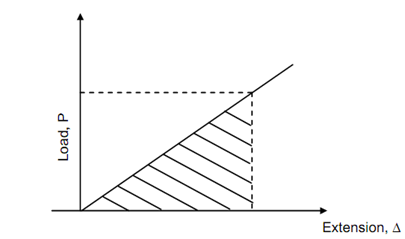
Figure

The strain energy per unit volumes is after referred to as resilience. The resilience at the yield point or proof stress is termed as proof resilience. The strain energy stored up to the fracture of the material is normally known as toughness.

In the previous units, it is seen that loads might be applied on a body in different modes, viz., as shear loads, as axial loads, as bending loads or as torsional loads.

In the following sections, we must derive expressions for the strain energy stored under each of the above forms of loading.