Components of Strain Energy Density:

You might recall in which the total stress field on an element might be considered as composed of two elements sets, one of which is the dilatation component and the other is the distortion component. Therefore, the net strain energy is also divided within two components, namely strain energy of dilatation, us and strain energy of distortion, u_d.

If the principal elements of stress field are given through σ₁, σ₂ and σ₃, we may write as,

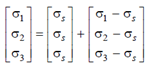
where the dilatation or spherical components of the stress field is given by

(σ₁ +σ₂ +σ₃)/3 or (σ_x +σ_y +σ_z)/3

Now let us acquired an expression for strain energy of distortion, using the form of Eq. (27).

u_d  = 1/2E [(σ₁- σ_s)² +( σ₂- σ_s)² +( σ₃- σ_s)²]

-2v[(σ₁- σ_s) ( σ₂- σ_s) +( σ₂- σ_s) ( σ₃- σ_s)+ ( σ₃- σ_s) ( σ₁- σ_s)]

=1/18E ({3 σ₁ -( σ₁+ σ₂+ σ₃)}² +{3 σ₂ -( σ₁+ σ₂+ σ₃)}² +{3 σ₃ -( σ₁+ σ₂+ σ₃)}² )

-2v({3 σ₁ -( σ₁+ σ₂+ σ₃)} ({3 σ₂ -( σ₁+ σ₂+ σ₃)} + . . . )

=1/18E ((2 σ₁- σ₂- σ₃)² +(2 σ₂- σ₁- σ₃)² +(2 σ₃- σ₁- σ₂)²

-2v{(2 σ₁- σ₂- σ₃) (2 σ₂- σ₃- σ₁) +(2 σ₂- σ₃- σ₁) (2 σ₃- σ₁- σ₂)

+(2 σ₃- σ₂- σ₁) (2 σ₁- σ₂- σ₃)})

=1/18E [6(σ₁² + σ₂² + σ₃²) -6 (σ₁ σ₂ + σ₂ σ₃+ σ₃ σ₁)

+6v(σ₁² + σ₂² + σ₃² - σ₁ σ₂ - σ₂ σ₃- σ₃ σ₁)

 =(1+v)3E [σ₁² + σ₂² + σ₃² - σ₁ σ₂ - σ₂ σ₃- σ₃ σ₁]

=2(1+v)6E [1/2 ((σ₁- σ₂)² +(σ₂- σ₃)² +(σ₃- σ₁)²)]

= 1/12E [(σ₁- σ₂)² +(σ₂- σ₃)² +(σ₃- σ₁)²]{as shear modulus, G = E/2(1+v)}                  . . . (29)

Thus, u_d  = 1/12G [(σ₁- σ₂)² +(σ₂- σ₃)² +(σ₃- σ₁)²]

u_d = 1/3G [(σ₁- σ₂/2)² + (σ₂- σ₃/2)² + (σ₃- σ₁/2)²]                                                        . . .(30)

Eq. (30) is more significant since the terms σ₁- σ₂/2, σ₂- σ₃/2 and σ₃- σ₁/2 represent the three extreme values of shear stress components.

The dilatation component of strain energy, us is not of much practical significance. However, if desired it may easily be obtained using the form of Eq. (27), as

u_s =1/2E(σ_s²+σ_s² +σ_s² -2v (σ_sσ_s +σ_sσ_s + σ_sσ_s))

i.e.  u_s =3/2E (σ_s² -2vσ_s²)

Or u_s = 3σ_s² (1-2v)/2E                                                                                                  . . . (31)

Or   u_s = σ_s²/2K                                                                                                                        . . . (32)

where, K is the Bulk Modulus given by E/3(1 - 2v)

The expression for strain energy density may be used to obtain, wherever required, to obtain the total strain energy by the expressions

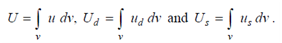
Like expressions have wide applications within structural analysis and theory of elasticity. Therefore, in analyzing the state of stress, energy density expressions have been found to be adequate.