Components of Strain Energy Density:
You might recall that the total stress field on an element might be considered as formed of two component sets, one of that is the dilatation component & the other is the distortion component. Therefore, the net strain energy is also divided into two components that is strain energy of dilatation, us and strain energy of distortion, ud.
If the principal components of stress field are given by s1, s2 and s3, we might write as,
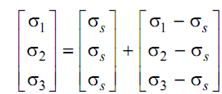
Where the dilatation or spherical components of the stress field ss is specified by
(s1 + s2 +s3 ) /3 or ( s1 + s2 +s3)/3
Now let us obtain an expression for strain energy of distortion, using the form of Eq.
ud = 1/2E [(s1 - ss )2 + (s2 - ss )2 +(s3 - ss )2
- 2v[(s1 - ss ) (s2 - ss )+ (s2 - ss ) (s3 - ss )+ (s3 - ss ) (s1 - ss )]
= 1/18E({3s1 -(s1 + s2 +s3 )}2 +{3s2 -(s1 + s2 +s3 )}2+{3s3 -(s1 + s2 +s3 )}2
-2v({3s1 -(s1 + s2 +s3 )} {3s2 -(s1 + s2 +s3 )}+ ...............)
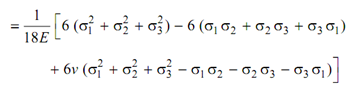
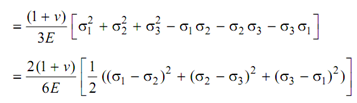
= 1/18E ((2s1 - s2 - s3 ) 2 +(2s2 - s2 - s3 ) 2 +(2s3 +-s1 - s2 ) 2
-2v {(2s1 - s2 - s3 ) (2s1 - s2 - s3 ) +(2s2 - s3 - s1 ) (2s3 - s1 - s2 )+ (2s3 - s2 - s1 ) (2s1 - s2 - s3 )})
1/2E[(s1-s2)2+(s2-s3)2+(s3-s1)2 [(as shear modulus, G=E/(2(1+v)
Therefore,
ud = 1/12G [(s1 - s2)2 + (s2 - s3)2 + (s3 - s1)2
ud = 1/3G [( (s1 - s2 )/2)2 + ((s2 - s3 )/2)2 + ((s3 - s1)/2 )2
Eq. is more important since the terms(s1 - s2 )/2 , (s2 - s3 )/2) and (s3 - s1)/2 represent the three extreme values of shear stress components.
The dilatation component of strain energy, us is not of much practical significance. Though, if desired it might easily be obtained by using the form of Eq. as
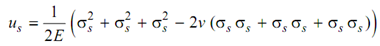
i.e.
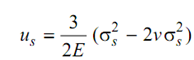
or 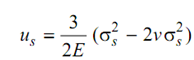
or 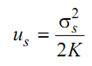
where, K is the Bulk Modulus specified by E/ (3(1 - 2v))
The expression for strain energy density might be utilized to obtain, wherever needed, to get the total strain energy by the expressions
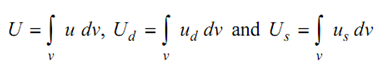
Such expressions have wide applications in structural analysis and theory of elasticity. However, in analysing the state of stress, energy density expressions have been found to be adequate.