Weibull Distribution (2-Parameter)

Weibull distribution fits in many cases where the hazard rate either increases or decreases, because this distribution has no characteristic shape. The probability density function for this distribution is expressed as

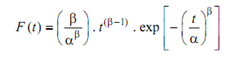
Where  β = Shape parameter;

α = Scale parameter;

Assuming γ = 0 (location parameter).

The Weibull cumulative distribution function is

F (t) = 1 - exp [- (t/  α ) ^β )]                        

T ≥ 0 and a, b ≥ 0

Reliability function is given by

R (t ) = 1 - F (t ) = exp [- (t/ α) ^β ]            

Therefore, 1 / [1 - F (t)] = exp [(t/ α) ^β]

Taking double logarithms

ln [ln{1/(1-F(t)}] = β ln (t ) - β ln α

This is a straight line of the form y = m x + c.

Thus the Weibull paper is constructed by having a log-reciprocal ordinate (y) scale representing cumulative probability of failure (or failure percentage) and the abscissa (x) scale representing the life value. The slope of the straight line plotted on this paper will be "β" the shape parameter.

The value of shape parameter defines the different phases of an item or system life characteristic as shown:

• β < 1 indicates decreasing failure rate or the phase of early failure.
• β = 1 indicates the constant failure rate or the normal useful operating life.
• β > 1 indicates the increasing failure rate or wear-out life of component.

Many standard statistical distributions are used to model the reliability parameters. But it has been found that a relatively small number of these distributions satisfy the needs and work most relatively.