Performing an experiment:

While performing an experiment for x² test more than 10,000 counts should always be collected in a definite time t and 15 / 20 / 25 counts are recorded in a consecutive manner in one sitting only. Following determinations should be made:

1. Calculate average count (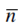), individual deviation (?) and the square of each deviation (x²). Sum of all deviations (∑?) should be nearly zero.

2. Calculate mean deviation (∑|?|)/N and standard deviation 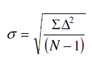 Compare σ with square root of mean 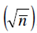which should be comparable.

3. Calculate Relative Standard Deviation, σ/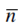 × 100.

4. Divide the mean deviation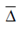 by standard deviation σ. The ratio should be nearly 0.8.

5. Count the number of times the counts are in the range.

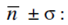It should be 65 - 70% of observations.

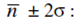It should be ~95% of observations.

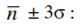It should be 99 - 100% of observations.

If any count exceeds then the counting system is not behaving properly or there is some gross error and the experiment should be repeated.

6. Arrange all the counts in ascending or descending order and calculate P (n) value for each observation. Now plot the counts on X-axis and P (n) on Y-axis. Draw a smooth Poisson distribution plot. It should look similar to Figure. The count corresponding to maximum P (n) should be comparable to the mean value . Larger the number of observations, the more precise will be the agreement.