Continuous Beam:

A third example of such a structure is the continuous beam ABCD which has a hinged support at A and roller supports at B, C and D. You are familiar with a simply supported beam AD which can be formed by removing the rollers at B and C and which is statically determinate. Now the beam AD is

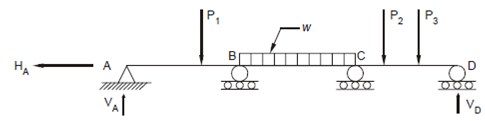
Figure: A Continuous Beam

having a hinged support at A (with two reaction components H_A and V_A) and the roller support at D (with the vertical reaction V_D) and is the same as simply supported beam with 3 unknown reaction (H_A, V_A, V_D) and can be solved by the 3 equations of equilibrium. However, the present beam with the additional supports at B and C providing additional reaction V_B and V_C (thus, total of five unknown reactions acting on the beam) cannot be solved by using equilibrium equations making it statically indeterminate again.

You may wonder why such structures are used at all, making matters more complicated. In fact, there are certain advantages in favour of statically indeterminate structures. As we shall see soon, in statically indeterminate structures bending moments and shearing forces induced are smaller in magnitude than in comparable statically determinate structures. These results in smaller and lighter sections accompanied with lesser costs, and cheaper construction. However, apart from computational difficulties, the statically indeterminate structures are subjected to internal stresses caused by differential settlement of supports, temperature changes and errors in exact fabrication of members, which are not perceptible in statically determinate structures. Thus, there are both advantages and disadvantages in such a construction. Also, indeterminacy is sometimes imposed by other considerations and cannot be avoided altogether. We now turn our attention to the analysis and solution of statically indeterminate structures.