Force Analysis without Friction:

As a first step, consider the friction is neglected. In the free body diagram illustrate in Figure 6(ii), force P is known by knowing the gas pressure & the diameter of the piston. In case of other two forces, the line of action is known. As friction force is neglected, the line of action of reaction F₁₄ is vertical. As there are only there forces, they need to pass through a common point (concurrent) for equilibrium to present. Examination of the free body diagram of link 3 (Figure 6(iii)) proves that the force F₄₃ contains line of action along AB because there are two forces only which have to be collinear. The collinear force may be in equilibrium if they are equivalent in magnitude and opposite in action. Then, the line of action of F₃₄ (= | F₄₃ |) is along link AB. To know about the magnitudes and directions of F₃₄ & F₁₄, polygon of forces may be formed by letting suitable scale or it may be determined analytically by using the following equations.

F ₃₄ cos φ= P or F =P/ cos φ⇒ F₃₄

F₃₄ sin φ= F₁₄ ⇒ F₁₄

(i)                                    (ii)

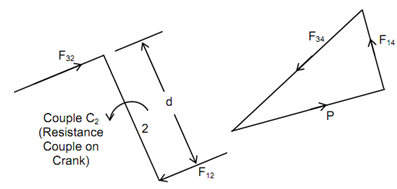
Figure(7)

By knowing the magnitude and direction of F₃₄, F₄₃ shall be known in magnitude and direction. The direction of F₄₃ will be opposite to F₃₄ & the magnitudes of these two shall be equal by Newton's third law that states that the action and reaction have the same magnitude and they are opposite in the line of action. F₃₂ shall be opposite to F₂₃ and they shall be equal in magnitude. In free body diagram of link 2, force F₁₂ will behave at the point O. The forces F₃₂ is acting at the point A (Figure 6(iv)). It may be observed that the forces F₃₂ and F₁₂ may not be collinear to keep link 2 in equilibrium. From the practical viewpoint it might not be so to resist overcoming load that is to be driven by the mechanism. As the reciprocating mechanism converts the linear motion to rotary motion crank 2 shall supply a turning moment to the load. Hence, F₁₂ need to be equivalent in magnitude to F₃₂ and opposite in direction to make a couple that has to counteract by the load couple C₂ to keep link 2 in equilibrium. It is illustrated in Figure 7(ii). The magnitude of the couple shall be (F₃₂ × d) where d is the area of the couple.