Effect of Sliding Friction:

 Mechanical Vibration because of the relative motion among the elements, frictional forces is produced. The links of a mechanism are linked mostly by either turning pairs or sliding pairs.

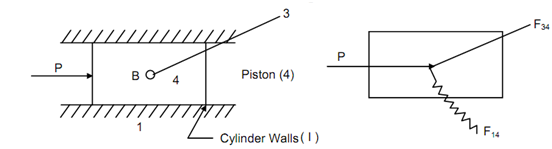
The Fig 1 (i) & (ii) indicates the piston subjected to the gas force 'P'. The connecting rod will apply the reactive force F₃₄ which behaves through the point B. These forces are not collinear thus; there need to be a third force that is reaction from the cylinder wall. This force 'F₁₄' is the consequential of normal reaction and force of friction.

The angle of inclination of F₁₄ along normal to the cylinder is 'φ' the angle of friction represent by

                                           φ= tan ^-1 μ            . . . (1)

here 'μ' = coefficient of friction.

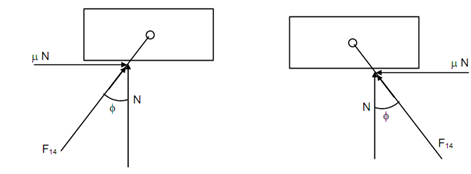
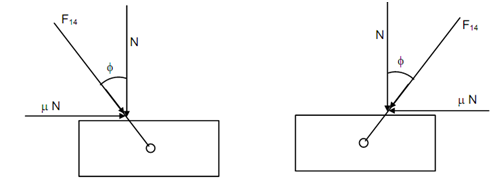
The maximum force of friction is μ N, here N is referring to the normal reaction. The different position of F₁₄ is illustrated in Figures (iii), (iv), (v) and (vi) based on direction of motion and the contact whether this is at the top or bottom.

                        (i)                                                              (ii)

        (iii)                                                         (iv)

   (v)                                                     (vi)

     Fig1

Some of links are linked through the turning pairs. We may consider two links 2 and 3 as illustrated in Fig1 (i). Let link 3 rotate clockwise w. r. t.  the link 2. As the friction opposes the relative motion it generates counter clockwise couple. The friction force along with normal reaction is illustrated in Figure (ii). These forces shall be the distributed forces at the contact area. Fig (iii) & (iv) show the vertical and horizontal components of tangential and radial forces at two symmetric points of the element of link 3. It shall be seen that the vertical components of the radial distributed load cancel with each other and horizontal components of tangential distributed load cancel with each other. Thus, there will be net reaction R_n and force of friction μ R_n. The force, exerted by link 2 on link 3 that means F₂₃ is given by following

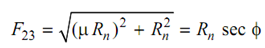                               . . . (2)

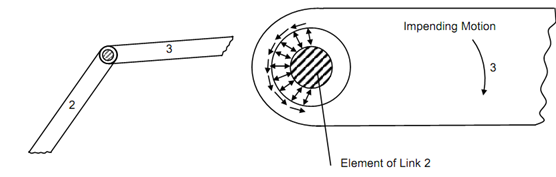
(i)                                                        (ii)

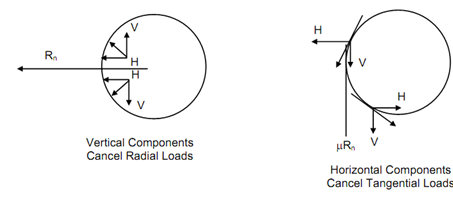
(iii)                                                                (iv))

Fig(2)

Assume'd' represent the diameter of the pint and r_f be the radius of friction circle

∴          μ Rn (d/2) = F₂₃ r_f                               . . . (3)

∴          R_n sec φ r_n = μ R_n (d/2) = tan φ R_n  (d/2)

∴          r_f   = (d/2) sin φ           . . . (4)

For small values of φ, values of sin φ and tan φ are nearly equal. So,

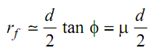                             . . . ( 5)

The force F₂₃ shall be tangential to the friction circle. The Figure (i) illustrates the different forces acting at the pin joint.

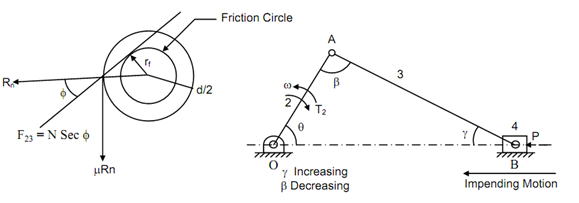
Fig (3)

A link that has pin joints at both of the ends.