Equivalent Dynamical System:

While motion occur, this is most desirable to replace a rigid body or link through two masses for dynamic analysis. It simplifies analysis. The corresponding dynamical system will have two point masses. The two mass system shall be equivalent dynamically to the rigid body if

(1) The entire body if the two masses of equivalent to the mass of the rigid body

That is                                           m₁ + m₂ = m                               . . . (6)

Here m₁ is mass of rigid body

         m₂ are point masses.

(2) The centre of gravity of the two of the masses is at the similar place as that of the rigid body

That means                        m₁ a = m₂ b                        . . . (7)

Here a & b respectively distances of m₁ & m₂ from centre of gravity,.

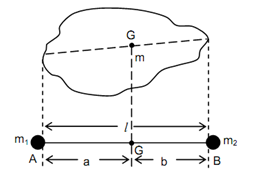
 Figure(11)

 (c)       The mass moment of inertia of the two masses system around an axis passing through centre of gravity 'G' is equivalent to the mass moment of inertia of the rigid body. That means

             m₁ a₂ + m₂ b₂ = m k ₂                            . . . (8)

here k is equal to radius of gyration of the rigid body around an axis through centre of gravity 'G'.

From equation (8) 

m₁ = m ₂ (b/2)

By putting value of m₁ in equation (8) we get the following

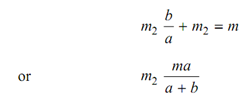
Likewise 

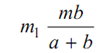
By substituting values of m₁ and m₂ in equation (8), we get the following

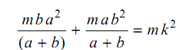
∴ k ₂  = a b                                       . . . (9)