Dynamic Force Analysis:

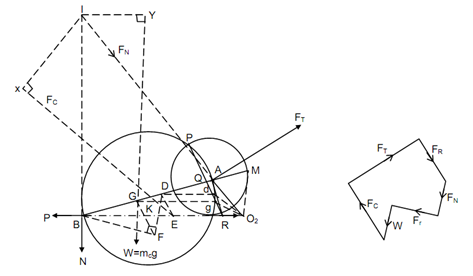
Figure 13(a) illustrates reciprocating engine mechanism O₂ AB. Assume:

m_p = Mass of reciprocating parts,

m_c = Mass of the connecting rod

N = Reaction at the cylinder wall,

F_r = Radial component of the force at the crank pin,

F_t = Tangential component of the force at the crank pin,

P = Net force at the piston along the line of stroke,

F_c = Inertia force on the connecting rod,

a_p = Acceleration of the reciprocating mass,

K = Radius of gyration of connecting rod, and

P = Gas force ± m_p a_p

Weight of connecting rod, W = m_c g.

Fig(13)

As acceleration of several points shall be needed, Kleins construction may be drawn and O₂AQR shows acceleration diagram. The process for drawing already this has been described earlier.

The connecting rod may be replaced by a dynamically corresponding system. One of the masses may be placed at the small end and the piston of the other mass may be estimated by using the following equation.

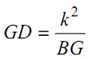                 . . . (12)

Here G being the centre of gravity. Point R may be joined along R to represent resultant acceleration of the connecting rod. The horizontal lines (means parallel to the line of stroke O₂B) may be drawn from points G & D to find out acceleration of these points. The acceleration of G & D are given by ω₂ O₂g and ω₂ O₂d, here ω being angular velocity of the crank. The length scale is similar as that of the configuration diagram.

           F_C = mc ω² O₂ g

Draw the lines of action of N and F_r so that they meet at point 'I'. From point D draw a line DE parallel to dO₂ to meet O₂B at E. The resulting inertia force on the connecting rod passes through point E. hence, draw a line from E parallel to gO₂ to define line of action of resultant inertia force 'F_C' on the connecting rod. The line of action of the weight 'W' might also be extended. Fall perpendiculars from I to the lines of action of F_C and W which are I X and I Y. To determine Ft, moment of different forces may be taken and the following equation is obtained.

             F_t I A = P × I B + F_C × I X + W × I Y                     . . . (13)

or 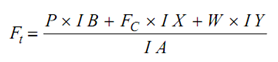       . . . (14)

To determine F_r and N, force polygon can be drawn as illustrated in Figure 13(b) that will give their magnitudes as their directions are already known.