Determine the magnitude of inertia torque on crank shaft:

The mass of reciprocating portion in a horizontal reciprocating engine is equal to 120 kg. The crank length is given as 90 mm and engine speed is equal to 600 rpm. Length and mass of the connecting rod is respectively 450 mm and 90 kg. The joint of connecting rod regarding its centre of gravity is equal to 150 mm. The distance of centre of gravity from little end is 180 mm. Determine the magnitude and sense of inertia torque on the crank shaft while the crank has turned 30^o from the inner-dead centre.

Solution

It is given:

Crank radius, 'r' = 90 mm = 0.09 m

Length of connecting rod, 'l' = 450 m = 0.45 m

Mass of reciprocating parts, 'm_r' = 120 kg

Mass of connecting rod, 'm_c' = 90 kg

Radius of gyration, 'k' = 150 mm = 0.15 m N = 600 rpm

 N=600rpm

∴          ω= 2π N /60

            = (2π× 60)/60 = 62.83 r/s

The configuration diagram of the reciprocating engine mechanism has been drawn in Figure 14 to an appropriate scale. Let one mass of the corresponding dynamical system is at small end and the other at point D

BG × GD = k ²

∴          GD = k ²/( BG) =( 150)² /180   =125 mm

Graphical construction may be drawn as described in Section 13.5. It is illustrated in Figure 14.

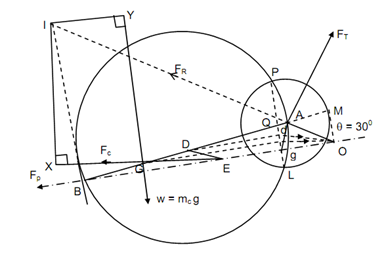
From Figure 14

IY = 0.179 m,                    I X = 0.215 m

I A = 0.517 m,                   I B = 0.303 m

Acceleration of connecting rod = 0.0854 m/s²

Acceleration of reciprocating parts, 'a_p' = 0.0871

Inertia force of the connecting rod.

F_C  = m_c w² a_c  = 90 × (62.83)2  × 0.0854 = 30341.32 N

W = 90 × g = 882.9 N

Inertia force of reciprocating parts

F_p  = m_r w² a p  = 120 × (62.83)² × 0.0871 = 41260.4 N

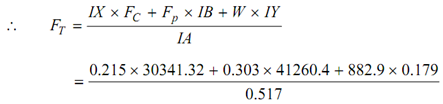
                    = 37152.22 N

Torque needed on crank shaft = 37152.22 × 0.09 = 3343.7 Nm (counterclockwise).