Correction Couple Applied To Two Mass System:

For two mass systems to be dynamically equal, it must satisfy all of the above mentioned three equations. Sometimes, the location of both of the masses is fixed as it is suitable in case of the relating rod of IC engines. One mass is supposed at the small ending and other at the big ending. In that case all of the equations may not be satisfied and the two mass systems will not be dynamically equivalent to the rigid body. The first two conditions only can be satisfied in this case but third condition will not be satisfied. This condition shall be satisfied if a couple is applied to the two mass systems. This couple is called as the correction couple.

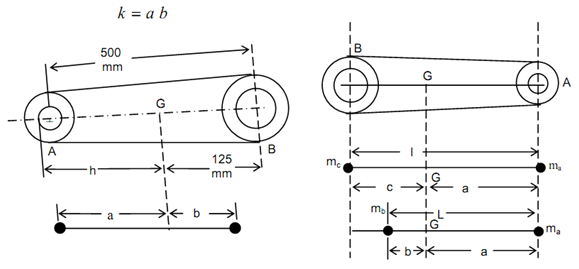
    Fig(12)

Figure 12 illustrate the connecting rod of an IC engine. This is of length 'l'. It is replaced through two lumped masses m_a and m_c respectively at the piston end and crank pin. In correspondent dynamical system of the connecting rod mass m_a is at the piston end and mass mc is among the crank pin and centre of gravity 'G'. The radius of gyration of the linking rod

As now the location of masses is fixed, hence, the new approximate radius of gyration is given by following

                                                                k₁ = a c

The difference in mass moment of inertia is specified by following

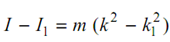                                                     . . . (10)

 If 'α' is angular acceleration of the connecting rod, the difference in inertia torque is given by following

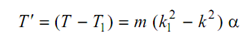
           = m (ac - ab) α = ma (c - b) α

or         T ′ = m a α (l - L)                                       . . . (11)

It is the correction couple that should be applied in case, the location of the two masses is fixed. Usually the magnitude of the correction couple is small and may be neglected, whenever, it is needless.