Determine the magnitude of torque:

A prismatic bar of hollow circular cross-section along outer & inner diameters 100 mm and 80 mm respectively, carries a bending moment of 5 kN-m. If the compressive, tensile,  and shear strengths of the material are specified as 140 N/mm², 125 N/mm² and 95 N/mm² respectively, what is the magnitude of torque that might safely be applied in addition to the bending moment.

Solution

Here, the criteria to be let are as:

s₁  ≤ 140 N/mm²

s₂  ≥ 125 N/mm²

t_max   ≥ 95 N/mm²

As the magnitudes of s₁ & s₂ for such bars shall be equal, we ought to satisfy only.

s2  ≥ - 125 N/mm2

t_max  ≥ 95 N/mm²

I for the section =  P/ 64(100⁴ - 80⁴ )= 2.898 x 10⁶  mm⁴

J for the section = P/32(100⁴  - 80⁴ )  = 5.796 x 10⁶  mm⁴

 Maximum compression due to bending moment,

-( M/I ) y _max =  - 5 x 10⁴ x50 / 2.898 x 10⁶ =  - 86.266 N/mm²

If T be the torque applied (in kN-m units), So,

t_max      =T x 10⁶ x 50/  5.796 x 10⁶ = 8.62664 T N/mm²           (under torsion alone)

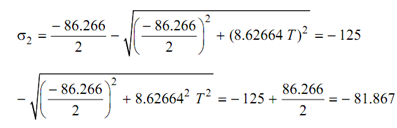
43.133²  + 8.62664² T ²  = (- 81.867)²

i.e.  

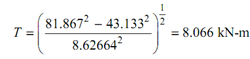
If the applied torque is in 8.066 kN-m, we are sure that the bar shall be safe in compression as well as tension.

Now ,we would analyse what torque shall have to be applied if t_max  ≥95 N/mm² .

We know that,

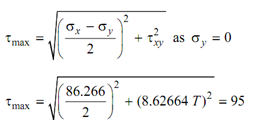
 (under combined bending and torsion)

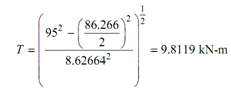
Though, we may not apply this much torque, as it shall cause compression failure. Therefore, the safe value of additional torque must be limited to 8.066 kN-m.