Example of Stability of Retaining Walls:

A masonry dam 8 m high is 1.5 m wide at the top and 5 m wide at the base. It retains water to a depth of 7.5m. A water face of the dam is vertical. Find out the maximum and minimum stresses at the base. The weight of the masonry is 22.4 kN/m³.

Solution

Consider 1 m width of the dam (Figure).

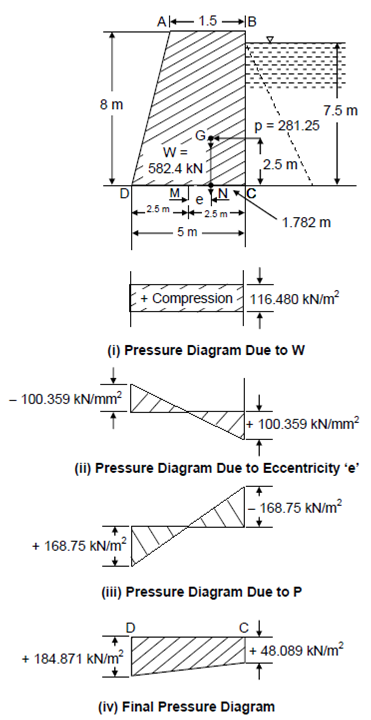
Figure

Weight of masonry, W = (1.5 + 5.0)/2× 8.0 × 22.4 = 582.4 kN

Its line of action meet the base DC at N here NC is

NC = x¯ = a²+ ab + b²/3(a + b) = 1.5² + 1.5 × 5 + 5²/3 (1.5 + 5) = 1.782 m

∴ Eccentricity, e = MN = MC - x¯ = 2.5 - 1.782 = 0.718 m

The horizontal water pressure P is

P = Wh²/2 =  10 × (7.5)²/2= 281.25 kN

and it acts at a height of 7.5/3 = 2.5 m above the base DC.

∴          (a)        Pressure due to weight W is

p₁ = W/b = 582.4/5 = 116.48 kN/m²

and is uniform at the base DC.

(b)       Pressure because of the eccentricity of weight W is

p₂   = ± 6We/b² = ± 6 × 582.4 × 0.718/5² = ± 100.359 kN/mm²

It varies from a tensile stress - 100.359 kN/m² at D to a compressive Stress + 100.359 kN/m² at C at base DC.

(c)        Pressure because of the moment of the horizontal water pressure p is

p₃   = ± 2 ph/b² = ± 2 × 281.25 × 7.5/5² = ± 168.750 kN/m²

which varies from a compressive stress at D to tensile at C. The final pressure diagram is shown in Figure 5(iv) as an algebraic sum of p1, p2, p3 and is 184.871 kN/m² (comp.) at D to 48.089 kN/m² (comp.) at C.