Design the section of a trapezoidal masonry dam:

Design the section of a trapezoidal masonry dam (with water face vertical) to impound water up to 29 m depth on the upstream side, with a free-board of 1 m. The maximum allowable pressure on base is 900 kN/m². Assume no tension in masonry (weight of masonry = 23 kN/m³).

Solution

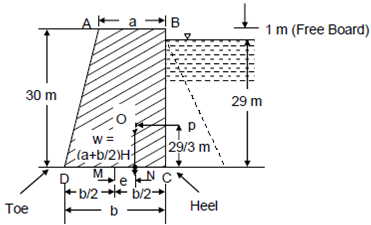
(Refer Figure 6)

Total height of dam = 29 + 1 = 30 m

Let the top width     = a metre

Base width    = b metre

Considering one metre length of dam.

Figure

Weight of masonry, W= a + b/2 ρ ⋅ H

= a + b/2 × 23 × 30

= 345 (a + b) kN

Maximum water pressure

P= wh²/2 = 10 × 29²/2 = 4205 kN

Maximum pressure at toe D

pD       = W/b - 6We/b² + 2Ph/b² = 900 kN/m²  (maximum allowable pressure)

Minimum pressure at heel C

pC   = W/b + 6 We/b² - 2Ph/b² = 0 (for no tension)

Substituting the values of W, P and h in the above equation

345 (a + b)/b - 6 × 345 (a + b) ⋅ e/b² +2 × 4205 × 29/b² = 900

345 (a + b)/b + 6 × 345 (a + b)/b² ⋅ e - 2 × 4205 × 29/b² = 0

Adding Eqs. (A) and (B), we get

2 × 345 (a + b/b) = 900,

Giving (a + b/b)

a + b/b = 1.304

or        a = 0.304 b

Subtracting Eq. (B) from Eq. (A) we get

2 × 6 × 345 (a + b)   e/ b² - 4 × 4205 × 29/b² = 900

- 4140 (a + b) e + 487780 = 900 b²

or        b² + 4.6 (a + b) e - 542 = 0

Also we know that

e + x¯ = b/2                                        [? MN + NC = MC = DC/2 ]

where x¯  =      a² + ab + b²/3(a + b)

Substituting the value of a

x¯ =       (0.304 b)² + 0.304 b² + b² /3 (0.304 b + b) = 0.357 b

∴          e = b/2 - x¯ = 0.5 b - 0.357 b = 0.143 b

Substituting the value of a and e in Eq. (C), we get

b² + 4.6 (0.304 b + b) (0.143 b) - 542 = 0

giving b = 17.17 m    ,          say 17.2 m

and     a = 0.304 b     ,           5.2 m (say)