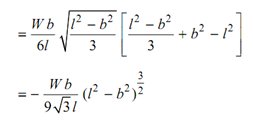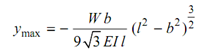Slope and deflection:

The slope and deflection shall be given by

EI (dy/dx) = (W b/2l) x²  - W [ x - a]²  + (Wb/6l) [b²  - l ² ]

EIy = (Wb/6l)  x³  - W [ x - a]³  + Wb [b²  - l ² ] x

Slope at A, (at x = 0), & noting that (W/2) [ x - a] is not applicable

 (dy/dx ) _A = θ _A   = - W b/6EIl [l ² - b²]

=- Wb / 6 EI l  [(a + b)²  - a² ] =- W a b/6 EI l (a + 2b)

Slope at B, (at x = l),

 (dy/dx)_B   θ _B = (W b/2l) . l ²  - (W/2) [l - a]²  + (W b/6l) [b²  - l ² ]

                       =  (Wb /6EI l) [3l ²  - 3b l + b²  - l ² ]

                            =  (Wb/6EI l)  [2 (a + b)²  - 3b (a + b) + b² ]

                                          =  (Wb/6EI l)  (2 a²  + ab) = (Wa b /6EI l)(2a + b)

or         θ_B  = (W a b /6EI l )(2a + b)

Deflection at centre ( x = l/2)  ,

EI y  = (Wb/6l) . (  l/2 )³- (W/6)  [ (l/2) - a]³ + W b/6l [b²  - l ² ] (l/2)

= W b l² /48 + (Wb/12) (b²  - l ² )

= (Wb/48) × [l ²  + 4b²  - 4l ² ]

= (Wb/48) × [4b²  - 3l ² ]

∴          y_C = ( Wb /48 EI)  × [4b²  - 3l ² ]

=-  (Wb/48 EI)  × [3l 2  - 4b2 ]

For deflection under the load y_w again  [ x - a]³  vanishes. Hence, by putting x = a

y_w  = Wb/6EI l [a³  + b² a - l ² a]

= (W a b /6EI l )[a²  + b²  - a²  - b²  - 2ab]

Y_w = W a² b²/3EIl

For maximum deflection,  dy/dx =0

0 = (Wb/2l ) x²  - (W/2) [0 - a]²  + Wb /6l [b²  - l ² ]

Wb/2l  . x²  = Wb / 6l[l ²  - b² ]

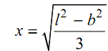
putting the value of x into the Equation, we may get

EIy _max = Wb x/ 6l [ x²  + b²  - l ² ]