Whals factor:

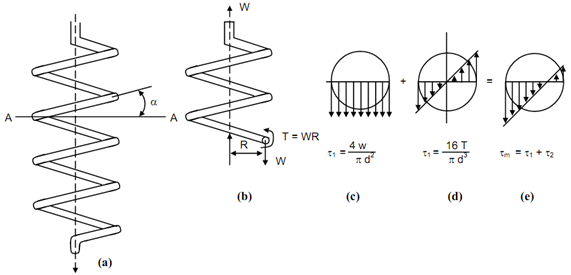
Figure: Close Coiled Helical Spring under Axial Load

Moment, T = W . R     ---------- (1)

 From Figure (b),

As described earlier, T can have two components :

 W R cos α       and W R sin α

But since α is small sin α→ 0 and cos α → 1.

Therefore,       T = W R           --------- (i)

But a direct shearing force W is also working upon the wire section.

Therefore, the wire section is subjected to direct shearing stress τ₁ and torsional shearing stress τ₂. The distributions of τ₁, τ₂ and concluded stress τ_m = τ₁ + τ₂ are illustrated in Figure (c).

τ = 4W/ π d²

τ = 16T/ π d³

∴          τ = (16/ π d ³) (WR + (Wd/4))

= (16WR/ π d ³ ) (1 +   (d /4R )

or,

τ _m = 16WR / π d ³   (1 +   d /2D)                    --------- . (2)

In such cases where d < < D,   d/2D can be neglected in comparison to 1. There

τ_m         = 16WR/ π d                            ------------ (3)

Otherwise τ_m is expressed as

τ _m        = K (16WR/ π d ³)-                        ------------ (4)

where K is refer to stress concentration factor on the inside of the coil. K is also called Whal's factor.

K =(1 +   d/2D)   ---------- (5)