Wilson-Hartnell Governor:

A Wilson-Hartnell governor is illustrated in given Figure. In this, the balls are associated by two springs that are known as main springs. The main springs are symmetrically arranged on either side of the sleeve. The balls are associated to the vertical arms of the two bell-crank levers. The horizontal arms of bell-crank levers hold two rollers at their ends. At the horizontal arm the rollers press against the sleeve. The bell-cranks rotate along the spindle. While speed enhances the ball-radius reduced, the springs exert an inward pull P on the balls and the rollers press against the sleeve that is raised.

An adjustable auxiliary spring (S) is connected to the sleeve by the means of a lever. The lever is pivoted at a fulcrum B. One of the ends of the lever is linked to the auxiliary spring while the other end of the lever fits into the groove in the sleeve. The auxiliary spring tends to remain the sleeve down.

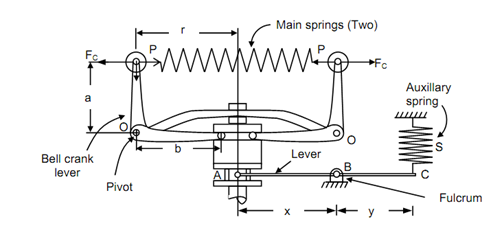
       Wilson-Hartnell Governor

Assume            m = Mass of each of ball in kg,

                                M = Mass of sleeve in kg,

W = Weight of sleeve = M × g in N,

P = Tension (or Pull) in the main spring in N,

S = Tension in the auxiliary spring in N,

FC = Centrifugal force of each ball in N,

r = Radius of rotation of balls in m,

s = Stiffness of auxiliary spring in N/m, and

s_a = Stiffness of auxiliary spring, in N/m.

The total downward force on the sleeve

= Weight of sleeve + force at lever ending A due to tension S in auxiliary spring (that is at point C)

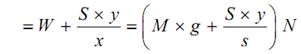
By taking the moments around the point 'O' of the bell-crank lever and neglecting the influence of the pull of gravity on the balls, we get the following

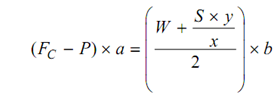
At the minimum speed 'ω₁', let

P₁ = Tension in main spring, S₁ = Tension in auxiliary spring & F_{C2 ,} P₂ and S₂ are equivalent values of centrifugal force, tension in main spring and tension in auxiliary spring equivalent to maximum speed, respectively.

By putting these values in above equation, we have for minimum speed, 'w₁'.

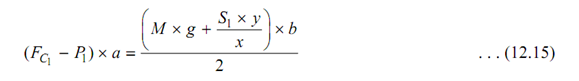
Likewise for maximum speed 'ω₂', we have the following

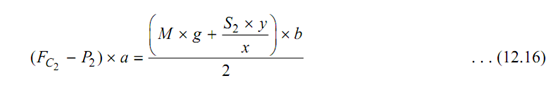
By subtracting equation (12.15) from equation (12.16), we have the following

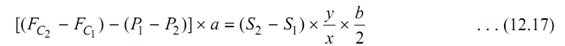
While the radius increases from r₁ to r₂, the ball springs shall be extended by the amount (d₂ - d₁) of 2 (r₂ - r₁) and auxiliary spring shall be extended by the amount 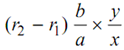The main spring consists of two springs.

∴          P₂ - P₁ = Net pull (or tension) in two main springs while radius increases from r₁ to r₂,

= 2 × Force exerted by each of the main spring,

= 2 × [stiffness of main spring × extension of ball springs],

= 2 × [s × 2 (r₂ - r₁)], and

= 4 × s × (r₂ - r₂) = 4s. (r₂ - r₁).

Likewise, extension in the auxiliary spring may also be estimated. The movement of the sleeve as radius modify r₁ to r₂

= b/a (r₂  - r₁ )

∴ Extension in the auxiliary spring

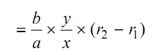
Assume the stiffness of the auxiliary spring be s_a.

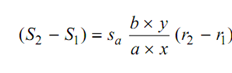
By substituting for (P₂ - P₁) and (S₂ - S₁) in equation (12.17)

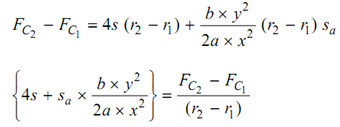   . . . (12.18)